


Next: O Americano, outra vez!
Up: Из Корнелла в Калтех
Previous: Ты их просто спрашиваешь?
Однажды в Принстоне я сидел в комнате отдыха и случайно
услышал, как математики говорят о ряде для 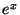 , который выглядит
как
, который выглядит
как
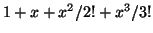 Каждый последующий член ряда
получается при умножении предыдущего члена на
Каждый последующий член ряда
получается при умножении предыдущего члена на 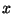 и его делении на
следующее порядковое число. Например, чтобы получить член,
следующий за
и его делении на
следующее порядковое число. Например, чтобы получить член,
следующий за 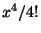 , нужно умножить этот член на
, нужно умножить этот член на 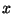 и разделить
на 5. Все очень просто.
Когда я был ребенком, я просто восхищался рядами и нередко
забавлялся с ними. С помощью ряда, о котором шла речь, я вычислял
и разделить
на 5. Все очень просто.
Когда я был ребенком, я просто восхищался рядами и нередко
забавлялся с ними. С помощью ряда, о котором шла речь, я вычислял
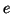 и видел, как быстро уменьшаются последующие члены.
Я пробормотал что-то вроде того, как легко можно вычислить
любую степень
и видел, как быстро уменьшаются последующие члены.
Я пробормотал что-то вроде того, как легко можно вычислить
любую степень 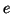 с помощью этого ряда (достаточно просто
подставить эту степень вместо
с помощью этого ряда (достаточно просто
подставить эту степень вместо 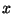 ).
-- Да? -- сказали они. «Отлично, чему равно
).
-- Да? -- сказали они. «Отлично, чему равно 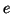 в степени 3,3?» --
спросил какой-то шутник. По-моему, это был Таки.
Я говорю: «Легко. 27,11».
Таки знает, что вычислить это в уме совсем нелегко.
«Эй! Как тебе это удалось?»
Другой парень говорит: «Ну вы же знаете Фейнмана, он просто
выдумал это число. На самом деле оно неправильное».
Они идут за таблицей, а я тем временем добавляю еще несколько
цифр. «27,1126», -- говорю я.
Они находят число в таблице. «Правильно! Но как ты это сделал?»
-- Я просто суммировал ряд.
-- Никто не умеет суммировать ряды так быстро. Ты, видимо,
просто знал это число. А чему равно
в степени 3,3?» --
спросил какой-то шутник. По-моему, это был Таки.
Я говорю: «Легко. 27,11».
Таки знает, что вычислить это в уме совсем нелегко.
«Эй! Как тебе это удалось?»
Другой парень говорит: «Ну вы же знаете Фейнмана, он просто
выдумал это число. На самом деле оно неправильное».
Они идут за таблицей, а я тем временем добавляю еще несколько
цифр. «27,1126», -- говорю я.
Они находят число в таблице. «Правильно! Но как ты это сделал?»
-- Я просто суммировал ряд.
-- Никто не умеет суммировать ряды так быстро. Ты, видимо,
просто знал это число. А чему равно 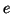 в степени 3?
-- Слушайте, -- говорю я. -- Это сложная работа! Я могу посчитать
только одну степень в день!
-- Ага! Это надувательство! -- обрадовались они.
-- О'кей, -- говорю я. -- 20,085.
Пока они ищут число в книжке, я добавляю еще несколько цифр.
Теперь они возбуждаются, потому что я правильно назвал еще одно
число.
Итак, все великие математики современности озадачены тем, как
мне удается подсчитать любую степень
в степени 3?
-- Слушайте, -- говорю я. -- Это сложная работа! Я могу посчитать
только одну степень в день!
-- Ага! Это надувательство! -- обрадовались они.
-- О'кей, -- говорю я. -- 20,085.
Пока они ищут число в книжке, я добавляю еще несколько цифр.
Теперь они возбуждаются, потому что я правильно назвал еще одно
число.
Итак, все великие математики современности озадачены тем, как
мне удается подсчитать любую степень 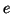 ! Один из них говорит: «Не
может быть, чтобы он просто подставлял это число
и суммировал ряд -- это слишком сложно.
Тут есть какой-то трюк. Ты не сможешь
вычислить какое угодно число, например,
! Один из них говорит: «Не
может быть, чтобы он просто подставлял это число
и суммировал ряд -- это слишком сложно.
Тут есть какой-то трюк. Ты не сможешь
вычислить какое угодно число, например, 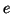 в степени 1,4».
Я говорю: «Да, работа не из легких. Но для вас, так и быть. 4,05».
Пока они ищут ответ, я добавляю еще несколько цифр и говорю:
«Все, на сегодня это последнее», и выхожу из комнаты.
Произошло же следующее. Я случайно знал три числа: натуральный
логарифм 10 (который нужен, чтобы переводить числа от основания 10
к основанию
в степени 1,4».
Я говорю: «Да, работа не из легких. Но для вас, так и быть. 4,05».
Пока они ищут ответ, я добавляю еще несколько цифр и говорю:
«Все, на сегодня это последнее», и выхожу из комнаты.
Произошло же следующее. Я случайно знал три числа: натуральный
логарифм 10 (который нужен, чтобы переводить числа от основания 10
к основанию 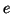 ), который равен 2,3026 (поэтому я знал, что
), который равен 2,3026 (поэтому я знал, что 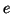 в
степени 2,3 примерно равно 10), а из-за радиоактивности (средняя
продолжительность жизни и период полураспада) я знал натуральный
логарифм 2, который равен 0,69315 (поэтому я также знал, что
в
степени 2,3 примерно равно 10), а из-за радиоактивности (средняя
продолжительность жизни и период полураспада) я знал натуральный
логарифм 2, который равен 0,69315 (поэтому я также знал, что 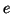 в
степени 0,7 равно почти 2). Кроме того, я знал, что
в
степени 0,7 равно почти 2). Кроме того, я знал, что 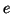 (в степени 1)
равно 2,71828.
Сначала меня попросили возвести
(в степени 1)
равно 2,71828.
Сначала меня попросили возвести 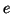 в степень 3,3. Это все равно,
что
в степень 3,3. Это все равно,
что 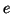 в степени 2,3 (то есть 10), умноженное на
в степени 2,3 (то есть 10), умноженное на 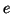 , то есть 27,18.
Пока они старались понять, как мне это удалось, я внес поправку на
лишние 0,0026: 2,3026 -- слегка завышенное число.
Я знал, что не смогу вычислить следующее число. Мне просто повезло,
когда парень назвал
, то есть 27,18.
Пока они старались понять, как мне это удалось, я внес поправку на
лишние 0,0026: 2,3026 -- слегка завышенное число.
Я знал, что не смогу вычислить следующее число. Мне просто повезло,
когда парень назвал 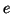 в степени 3: это
в степени 3: это 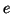 в степени 2,3, умноженное
на
в степени 2,3, умноженное
на 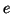 в степени 0,7 (или 10, умноженное на 2). Итак, я знал, что это 20
с чем-то, а пока они раздумывали над тем, как мне это удалось, я внес
поправку на 0,693.
Ну уж теперь-то я был уверен, что не смогу вычислить следующее
число, но мне опять повезло. Парень попросил посчитать е в степени
1,4, а это
в степени 0,7 (или 10, умноженное на 2). Итак, я знал, что это 20
с чем-то, а пока они раздумывали над тем, как мне это удалось, я внес
поправку на 0,693.
Ну уж теперь-то я был уверен, что не смогу вычислить следующее
число, но мне опять повезло. Парень попросил посчитать е в степени
1,4, а это 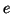 в степени 0,7, умноженное на само себя. Так что все, что
мне пришлось сделать, так это чуть-чуть подкорректировать четверку!
Они так никогда и не поняли, как мне это удалось.
Когда я был в Лос-Аламосе, я обнаружил, что Ханс Бете умеет
превосходно считать. Например, как-то раз мы подставляли числа в
формулу и дошли до возведения в квадрат числа 48. Я потянулся за
калькулятором Маршан, он же сказал: «Это 2300». Я начинаю
нажимать кнопки, а он говорит: «Если тебе нужно знать точно, то ответ
2304».
Машина говорит 2304. «Класс! Это же просто здорово!» -- говорю я.
-- Разве ты не знаешь, как возводят в квадрат числа, близкие к 50? --
говорит он. -- Возводишь в квадрат 50, это 2500, а потом вычитаешь
100, умноженное на разность нужного тебе числа и 50 (в данном случае
эта разность равна 2), получается 2300. Если хочешь получить точный
результат, возведи эту разность в квадрат и прибавь к полученному
числу. Так и получается 2304.
Через несколько минут нам понадобилось взять кубический корень
из 2,5. Чтобы взять кубический корень с помощью калькулятора
Маршан, нужно воспользоваться таблицей для первого приближения. Я
открываю ящик, чтобы взять эту таблицу, -- на этот раз времени
требуется немного больше, -- а он говорит: «Примерно 1,35».
Я проверяю результат на Маршане, и он оказывается правильным.
«А как ты это сделал? -- спрашиваю я. -- Ты владеешь секретом того,
как брать кубический корень из числа?»
-- О, -- говорит он, -- логарифм 2,5 равен стольки-то. Треть этого
логарифма находится между логарифмом 1,3, который равен стольки-то,
и логарифмом 1,4, который равен стольки-то, так что я просто
применил метод интерполяции.
Итак, кое-что я выяснил: во-первых, он наизусть знает таблицы
логарифмов, а во-вторых, один только объем арифметических
действий, которые он проделал во время интерполяции, отнял бы у
меня больше времени, чем если бы я просто подошел к столу и
понажимал кнопки калькулятора. На меня это произвело колоссальное
впечатление.
После этого я тоже пытался проделать что-либо подобное. Я запомнил
значения нескольких логарифмов и начал
замечать, что происходит. Например, если кто-то
спрашивает: «Чему равно 28 в квадрате?», замечаешь, что квадратный
корень из двух равен 1,4, а 28 -- это 20, умноженное на 1,4, поэтому 28
в квадрате должно примерно равняться 400, умноженному на 2, или
800.
Если кто-нибудь спрашивает, сколько получится, если разделить 1
на 1,73, то можно сразу ответить, что 0,577, потому что знаешь, что
1,73 -- это почти квадратный корень из 3, поэтому 1/1,73 равно одной
трети квадратного корня из 3. А если нужно определить отношение
1/1,75, оно равно величине обратной дроби 7/4, а вы помните, что если
в знаменателе стоит 7, то десятичные цифры повторяются: 0,571428...
Меня очень забавляли мои собственные попытки быстрого
выполнения арифметических действий с помощью хитрых приемов, а в
особенности состязание с Хансом. Однако заметить что-либо, что
упустил он, и указать ему на ответ мне удавалось крайне редко, но,
когда все же удавалось, он от души смеялся. Он обладал уникальной
способностью почти всегда находить ответ на любую задачу в
пределах одного процента. Для него это не составляло особой
сложности: каждое число было близко к какому-то другому, которое он
знал.
Однажды я пребывал в особенно хорошем расположении духа. В
техническом отделе был обеденный перерыв, и я не знаю, как такая
идея могла прийти мне в голову, но я заявил: «За шестьдесят секунд я
могу дать ответ с точностью до 10 процентов на любую задачу,
которую кто-либо сумеет сформулировать за десять секунд!»
Люди начали давать мне задачи, которые казались им сложными,
например, проинтегрировать функцию типа
в степени 0,7, умноженное на само себя. Так что все, что
мне пришлось сделать, так это чуть-чуть подкорректировать четверку!
Они так никогда и не поняли, как мне это удалось.
Когда я был в Лос-Аламосе, я обнаружил, что Ханс Бете умеет
превосходно считать. Например, как-то раз мы подставляли числа в
формулу и дошли до возведения в квадрат числа 48. Я потянулся за
калькулятором Маршан, он же сказал: «Это 2300». Я начинаю
нажимать кнопки, а он говорит: «Если тебе нужно знать точно, то ответ
2304».
Машина говорит 2304. «Класс! Это же просто здорово!» -- говорю я.
-- Разве ты не знаешь, как возводят в квадрат числа, близкие к 50? --
говорит он. -- Возводишь в квадрат 50, это 2500, а потом вычитаешь
100, умноженное на разность нужного тебе числа и 50 (в данном случае
эта разность равна 2), получается 2300. Если хочешь получить точный
результат, возведи эту разность в квадрат и прибавь к полученному
числу. Так и получается 2304.
Через несколько минут нам понадобилось взять кубический корень
из 2,5. Чтобы взять кубический корень с помощью калькулятора
Маршан, нужно воспользоваться таблицей для первого приближения. Я
открываю ящик, чтобы взять эту таблицу, -- на этот раз времени
требуется немного больше, -- а он говорит: «Примерно 1,35».
Я проверяю результат на Маршане, и он оказывается правильным.
«А как ты это сделал? -- спрашиваю я. -- Ты владеешь секретом того,
как брать кубический корень из числа?»
-- О, -- говорит он, -- логарифм 2,5 равен стольки-то. Треть этого
логарифма находится между логарифмом 1,3, который равен стольки-то,
и логарифмом 1,4, который равен стольки-то, так что я просто
применил метод интерполяции.
Итак, кое-что я выяснил: во-первых, он наизусть знает таблицы
логарифмов, а во-вторых, один только объем арифметических
действий, которые он проделал во время интерполяции, отнял бы у
меня больше времени, чем если бы я просто подошел к столу и
понажимал кнопки калькулятора. На меня это произвело колоссальное
впечатление.
После этого я тоже пытался проделать что-либо подобное. Я запомнил
значения нескольких логарифмов и начал
замечать, что происходит. Например, если кто-то
спрашивает: «Чему равно 28 в квадрате?», замечаешь, что квадратный
корень из двух равен 1,4, а 28 -- это 20, умноженное на 1,4, поэтому 28
в квадрате должно примерно равняться 400, умноженному на 2, или
800.
Если кто-нибудь спрашивает, сколько получится, если разделить 1
на 1,73, то можно сразу ответить, что 0,577, потому что знаешь, что
1,73 -- это почти квадратный корень из 3, поэтому 1/1,73 равно одной
трети квадратного корня из 3. А если нужно определить отношение
1/1,75, оно равно величине обратной дроби 7/4, а вы помните, что если
в знаменателе стоит 7, то десятичные цифры повторяются: 0,571428...
Меня очень забавляли мои собственные попытки быстрого
выполнения арифметических действий с помощью хитрых приемов, а в
особенности состязание с Хансом. Однако заметить что-либо, что
упустил он, и указать ему на ответ мне удавалось крайне редко, но,
когда все же удавалось, он от души смеялся. Он обладал уникальной
способностью почти всегда находить ответ на любую задачу в
пределах одного процента. Для него это не составляло особой
сложности: каждое число было близко к какому-то другому, которое он
знал.
Однажды я пребывал в особенно хорошем расположении духа. В
техническом отделе был обеденный перерыв, и я не знаю, как такая
идея могла прийти мне в голову, но я заявил: «За шестьдесят секунд я
могу дать ответ с точностью до 10 процентов на любую задачу,
которую кто-либо сумеет сформулировать за десять секунд!»
Люди начали давать мне задачи, которые казались им сложными,
например, проинтегрировать функцию типа 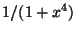 , которая
практически не изменяется в названном ими диапазоне. Самой сложной
задачей, которую мне дали, было определить биномиальный
коэффициент
, которая
практически не изменяется в названном ими диапазоне. Самой сложной
задачей, которую мне дали, было определить биномиальный
коэффициент 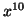 в выражении
в выражении 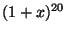 . Я это сделал ровно
за 60 секунд.
Все давали мне задачи, я чувствовал себя великим, когда в столовую
вошел Пол Олам. До приезда в Лос-Аламос какое-то время Пол
работал вместе со мной в Принстоне и всегда оказывался умнее меня.
Например, однажды я в рассеянности играл одной из мерных лент,
которые при нажатии кнопки, возвращаясь в рулетку, врезаются в руку.
Лента все время слегка поворачивалась, и мне было немного больно.
«Ой! -- воскликнул я. -- Ну и осел же я. Я продолжаю играть с этой
штукой, а она каждый раз причиняет мне боль».
Он сказал: «Ты ее неправильно держишь», взял эту чертову штуковину,
вытащил ленту, нажал кнопку, и она вернулась точно на место, не
причинив ему боли.
-- Здорово! Как ты это делаешь? -- воскликнул я.
-- Догадайся!
В течение следующих двух недель я хожу по Принстону, щелкая
рулеткой и пытаясь загнать ленту на место, до тех пор пока на моей
руке не остается живого места. Наконец, мое терпение лопает. «Поль!
Я сдаюсь! Как, черт побери, ты держишь эту штуковину, что она не
ранит твою руку?»
-- А кто говорил, что не ранит? Мне тоже бывает больно!
Я почувствовал себя полным идиотом. Он сумел сделать так, что я
две недели издевался над своей рукой!
Так вот, Пол проходит по столовой, где все просто стоят на ушах.
«Эй, Пол! -- кричат они. -- Фейнман -- просто супер! Мы даем ему
задачу, которую можно сформулировать за десять секунд, и он за одну
минуту дает ответ с точностью до 10 процентов. Дай ему какую-нибудь
задачу!»
Почти не останавливаясь, он говорит: «Тангенс 10 градусов в сотой
степени».
Я влип: для этого нужно делить на число пи до ста десятичных
разрядов! Это было безнадежно!
Однажды я похвастался: «Я могу решить любой интеграл, который
все остальные могут решить только с помощью интегрирования по
контуру, другими способами».
Тогда Пол пишет мне просто огромный чертов интеграл, который он
получил, начав с комплексной функции, ответ которой он знал. Он
убрал вещественную часть этой функции и оставил лишь мнимую. Он
развернул функцию так, что единственным возможным способом
решения интеграла осталось интегрирование по контуру! Он все время
подставлял мне такие подножки. Он был очень умен.
Когда я впервые попал в Бразилию, я как-то раз обедал, не помню
во сколько, -- я постоянно приходил в ресторан не вовремя, --
поэтому и оказался единственным посетителем. Я ел рис с бифштексом
(который обожал), а неподалеку стояли четыре официанта.
Тут в ресторан вошел японец. Я уже раньше видел его: он бродил по
городу, пытаясь продать счеты. Он начал разговаривать с официантами
и бросил им вызов, заявив, что может складывать числа быстрее, чем
любой из них.
Официанты не хотели потерять лицо, поэтому сказали: «Да, да,
конечно. А почему бы Вам не пойти к тому посетителю и не устроить
соревнование с ним?»
Этот человек подошел ко мне. Я попытался
сопротивляться: «Я плохо говорю на португальском!»
Официанты засмеялись. «С числами это не имеет значения», -- сказали
они.
Они принесли мне карандаш и бумагу.
Человек попросил официанта назвать несколько чисел, которые
нужно сложить. Он разбил меня наголову, потому что пока я писал
числа, он уже складывал их.
Тогда я предложил, чтобы официант написал два одинаковых
списка чисел и отдал их нам одновременно. Разница оказалась
небольшой. Он опять выиграл у меня приличное время.
Однако японец вошел в раж: он хотел показать, какой он умный.
«Multiplicao!28.1» --
сказал он.
Кто-то написал задачу. Он снова выиграл у меня, хотя и не так
много, потому что я довольно прилично умею умножать.
А потом этот человек сделал ошибку: он предложил деление. Он не
понимал одного: чем сложнее задача, тем у меня больше шансов
победить.
Нам дали длинную задачу на деление. Ничья.
Это весьма обеспокоило японца, потому что он явно прекрасно умел
выполнять арифметические операции с помощью счет, а тут его почти
победил какой-то посетитель ресторана.
«Raios cubicos!» -- мстительно говорит он. Кубические корни! Он
хочет брать кубические корни с помощью арифметики! Трудно найти
более сложную фундаментальную задачу в арифметике. Должно быть,
это был его конек в упражнениях со счетами.
Он пишет на бумаге число -- любое большое число -- я до сих пор
его помню: 1729,03. Он начинает работать с этим числом и при этом
что-то бормочет и ворчит: «Бу-бу-бу-хм-гм-бу-бу», -- он трудится как
демон! Он просто погружается в этот кубический корень!
Я же тем временем просто сижу на своем месте.
Один из официантов говорит: «Что Вы делаете?»
Я указываю на голову. «Думаю!» -- говорю я. Затем пишу на бумаге
12. Еще через какое-то время -- 12,002.
Человек со счетами вытирает со лба пот и говорит: «Двенадцать!»
«О, нет! -- возражаю я. -- Больше цифр! Больше цифр!» Я знаю,
что, когда с помощью арифметики берешь кубический корень, то
каждая последующая цифра требует большего труда, чем предыдущая.
Это работа не из легких.
Он опять уходит в работу и при этом бормочет: «Уф-фыр-хм-уф-хм-гм...».
Я же добавляю еще две цифры. Наконец, он поднимает голову и
говорит: «12,0!»
Официанты просто светятся от счастья. Они говорят японцу:
«Смотрите! Он делает это в уме, а Вам нужны счеты! И цифр у него
больше!»
Он был абсолютно измотан и ушел, побежденный и униженный.
Официанты поздравили друг друга.
Каким же образом посетитель выиграл у счетов? Число было
1729,03. Я случайно знал, что в кубическом футе 1728 кубических
дюймов, так что было ясно, что ответ немногим больше 12. Излишек
же, равный 1,03, -- это всего лишь одна часть из почти 2000, а во время
курса исчисления я запомнил, что для маленьких дробей излишек
кубического корня равен одной трети излишка числа. Так что мне
пришлось лишь найти дробь 1/1728, затем умножить полученный
результат на 4 (разделить на 3 и умножить на 12). Вот так мне удалось
получить целую кучу цифр.
Несколько недель спустя этот человек вошел в бар того отеля, в
котором я остановился. Он узнал меня и подошел. «Скажите мне, --
спросил он, -- как Вам удалось так быстро решить задачу с
кубическим корнем?»
Я начал объяснять, что использовал приближенный метод, и мне
достаточно было определить процент ошибки. «Допустим, Вы дали
мне число 28. Кубический корень из 27 равен 3...»
Он берет счеты: жжжжжжжжжжжжжжжж -- «Да», -- соглашается
он.
И тут до меня доходит: он не знает чисел. Когда у тебя есть счеты,
не нужно запоминать множество арифметических комбинаций; нужно
просто научится щелкать костяшками вверх-вниз. Нет необходимости
запоминать, что 9 + 7 = 16; ты просто знаешь, что когда прибавляешь 9,
то нужно передвинуть десятичную костяшку вверх, а единичную --
вниз. Поэтому основные арифметические действия мы выполняем
медленнее, зато мы знаем числа.
Более того, сама идея о приближенном методе вычисления была за
пределами его понимания, несмотря на то, что зачастую невозможно
найти метод точного вычисления кубического корня. Поэтому мне так
и не удалось научить его брать кубический корень или объяснить, как
мне повезло, что он выбрал число 1729,03.
. Я это сделал ровно
за 60 секунд.
Все давали мне задачи, я чувствовал себя великим, когда в столовую
вошел Пол Олам. До приезда в Лос-Аламос какое-то время Пол
работал вместе со мной в Принстоне и всегда оказывался умнее меня.
Например, однажды я в рассеянности играл одной из мерных лент,
которые при нажатии кнопки, возвращаясь в рулетку, врезаются в руку.
Лента все время слегка поворачивалась, и мне было немного больно.
«Ой! -- воскликнул я. -- Ну и осел же я. Я продолжаю играть с этой
штукой, а она каждый раз причиняет мне боль».
Он сказал: «Ты ее неправильно держишь», взял эту чертову штуковину,
вытащил ленту, нажал кнопку, и она вернулась точно на место, не
причинив ему боли.
-- Здорово! Как ты это делаешь? -- воскликнул я.
-- Догадайся!
В течение следующих двух недель я хожу по Принстону, щелкая
рулеткой и пытаясь загнать ленту на место, до тех пор пока на моей
руке не остается живого места. Наконец, мое терпение лопает. «Поль!
Я сдаюсь! Как, черт побери, ты держишь эту штуковину, что она не
ранит твою руку?»
-- А кто говорил, что не ранит? Мне тоже бывает больно!
Я почувствовал себя полным идиотом. Он сумел сделать так, что я
две недели издевался над своей рукой!
Так вот, Пол проходит по столовой, где все просто стоят на ушах.
«Эй, Пол! -- кричат они. -- Фейнман -- просто супер! Мы даем ему
задачу, которую можно сформулировать за десять секунд, и он за одну
минуту дает ответ с точностью до 10 процентов. Дай ему какую-нибудь
задачу!»
Почти не останавливаясь, он говорит: «Тангенс 10 градусов в сотой
степени».
Я влип: для этого нужно делить на число пи до ста десятичных
разрядов! Это было безнадежно!
Однажды я похвастался: «Я могу решить любой интеграл, который
все остальные могут решить только с помощью интегрирования по
контуру, другими способами».
Тогда Пол пишет мне просто огромный чертов интеграл, который он
получил, начав с комплексной функции, ответ которой он знал. Он
убрал вещественную часть этой функции и оставил лишь мнимую. Он
развернул функцию так, что единственным возможным способом
решения интеграла осталось интегрирование по контуру! Он все время
подставлял мне такие подножки. Он был очень умен.
Когда я впервые попал в Бразилию, я как-то раз обедал, не помню
во сколько, -- я постоянно приходил в ресторан не вовремя, --
поэтому и оказался единственным посетителем. Я ел рис с бифштексом
(который обожал), а неподалеку стояли четыре официанта.
Тут в ресторан вошел японец. Я уже раньше видел его: он бродил по
городу, пытаясь продать счеты. Он начал разговаривать с официантами
и бросил им вызов, заявив, что может складывать числа быстрее, чем
любой из них.
Официанты не хотели потерять лицо, поэтому сказали: «Да, да,
конечно. А почему бы Вам не пойти к тому посетителю и не устроить
соревнование с ним?»
Этот человек подошел ко мне. Я попытался
сопротивляться: «Я плохо говорю на португальском!»
Официанты засмеялись. «С числами это не имеет значения», -- сказали
они.
Они принесли мне карандаш и бумагу.
Человек попросил официанта назвать несколько чисел, которые
нужно сложить. Он разбил меня наголову, потому что пока я писал
числа, он уже складывал их.
Тогда я предложил, чтобы официант написал два одинаковых
списка чисел и отдал их нам одновременно. Разница оказалась
небольшой. Он опять выиграл у меня приличное время.
Однако японец вошел в раж: он хотел показать, какой он умный.
«Multiplicao!28.1» --
сказал он.
Кто-то написал задачу. Он снова выиграл у меня, хотя и не так
много, потому что я довольно прилично умею умножать.
А потом этот человек сделал ошибку: он предложил деление. Он не
понимал одного: чем сложнее задача, тем у меня больше шансов
победить.
Нам дали длинную задачу на деление. Ничья.
Это весьма обеспокоило японца, потому что он явно прекрасно умел
выполнять арифметические операции с помощью счет, а тут его почти
победил какой-то посетитель ресторана.
«Raios cubicos!» -- мстительно говорит он. Кубические корни! Он
хочет брать кубические корни с помощью арифметики! Трудно найти
более сложную фундаментальную задачу в арифметике. Должно быть,
это был его конек в упражнениях со счетами.
Он пишет на бумаге число -- любое большое число -- я до сих пор
его помню: 1729,03. Он начинает работать с этим числом и при этом
что-то бормочет и ворчит: «Бу-бу-бу-хм-гм-бу-бу», -- он трудится как
демон! Он просто погружается в этот кубический корень!
Я же тем временем просто сижу на своем месте.
Один из официантов говорит: «Что Вы делаете?»
Я указываю на голову. «Думаю!» -- говорю я. Затем пишу на бумаге
12. Еще через какое-то время -- 12,002.
Человек со счетами вытирает со лба пот и говорит: «Двенадцать!»
«О, нет! -- возражаю я. -- Больше цифр! Больше цифр!» Я знаю,
что, когда с помощью арифметики берешь кубический корень, то
каждая последующая цифра требует большего труда, чем предыдущая.
Это работа не из легких.
Он опять уходит в работу и при этом бормочет: «Уф-фыр-хм-уф-хм-гм...».
Я же добавляю еще две цифры. Наконец, он поднимает голову и
говорит: «12,0!»
Официанты просто светятся от счастья. Они говорят японцу:
«Смотрите! Он делает это в уме, а Вам нужны счеты! И цифр у него
больше!»
Он был абсолютно измотан и ушел, побежденный и униженный.
Официанты поздравили друг друга.
Каким же образом посетитель выиграл у счетов? Число было
1729,03. Я случайно знал, что в кубическом футе 1728 кубических
дюймов, так что было ясно, что ответ немногим больше 12. Излишек
же, равный 1,03, -- это всего лишь одна часть из почти 2000, а во время
курса исчисления я запомнил, что для маленьких дробей излишек
кубического корня равен одной трети излишка числа. Так что мне
пришлось лишь найти дробь 1/1728, затем умножить полученный
результат на 4 (разделить на 3 и умножить на 12). Вот так мне удалось
получить целую кучу цифр.
Несколько недель спустя этот человек вошел в бар того отеля, в
котором я остановился. Он узнал меня и подошел. «Скажите мне, --
спросил он, -- как Вам удалось так быстро решить задачу с
кубическим корнем?»
Я начал объяснять, что использовал приближенный метод, и мне
достаточно было определить процент ошибки. «Допустим, Вы дали
мне число 28. Кубический корень из 27 равен 3...»
Он берет счеты: жжжжжжжжжжжжжжжж -- «Да», -- соглашается
он.
И тут до меня доходит: он не знает чисел. Когда у тебя есть счеты,
не нужно запоминать множество арифметических комбинаций; нужно
просто научится щелкать костяшками вверх-вниз. Нет необходимости
запоминать, что 9 + 7 = 16; ты просто знаешь, что когда прибавляешь 9,
то нужно передвинуть десятичную костяшку вверх, а единичную --
вниз. Поэтому основные арифметические действия мы выполняем
медленнее, зато мы знаем числа.
Более того, сама идея о приближенном методе вычисления была за
пределами его понимания, несмотря на то, что зачастую невозможно
найти метод точного вычисления кубического корня. Поэтому мне так
и не удалось научить его брать кубический корень или объяснить, как
мне повезло, что он выбрал число 1729,03.



Next: O Americano, outra vez!
Up: Из Корнелла в Калтех
Previous: Ты их просто спрашиваешь?
Anthon
2003-05-22